Électricité générale
0.1 INTRODUCTION
0.1.1 Connaissance préalable
La matière de ce module rejoint la matière de l’enseignement secondaire. Les
étudiants de l’enseignement secondaire général vont trouver la matière dans leurs
cours de physique. Les étudiants d’un enseignement technique ou industriel ont
peut-être déjà vu toute la matière. Les étudiants pour lesquels la matière est nouvelle sont encouragés de bien étudier la matière, ceci est une condition essentielle
pour savoir suivre la matière dans les modules suivantes.
0.1.2 Livre d’étude
Pendant les trois ans qui vont suivre, on va utiliser le livre d’étude suivant [Wildi, 2006]
Electrical Machines, Drives, and Power Systems Theodore Wildi ISBN 0-13-
196918-8.
0.1.3 Cours
Les cours et toutes informations concernant les leçons se trouvent ici http://magelhaes.hzs.be/willem
Dans l’electricité et dans l’électronique ont choisit de rendre le chiffres avec pre-
fix. On va presque jamais rencontrer la notation scientifique (utilisé en physique)
dans notre spécialité. Un courant de 0,012A on utilise 12mA (=12 x 10−3A) au
lieu de 1,2 x 10−2A On va jamais écrire 0, 15mV . mais on ecrit 150µV.
0.2 COURANT TENSION ET RÉSISTANCE
0.2.1 Charge,Q (Coulomb, C)
Le coulomb est l’unité de charge électrique dans le système international (SI).
C’est une unité dérivée. Son nom vient de celui du physicien français Charles de
Coulomb.
D’après la loi de Coulomb, deux charges ponctuelles d’un coulomb chacune
et séparées d’un mètre dans le vide exercent l’une sur l’autre une force de
9x109 N, c’est-à-dire approximativement le poids d’un objet de 900000000
kg.
On peut dire aussi que:
Un coulomb c’est la quantité d’électricité traversant une section d’un conducteur parcouru par un courant d’intensité de 1 ampère pendant 1 seconde
(1C = 1A x 1s). Elle est équivalente à 6,24150962915265x1018 charges élémentaires.
0.2.2 Courant, I (Ampère, A)
Un courant électrique est un déplacement d’ensemble de porteurs de charge électrique, généralement des électrons, au sein d’un matériau conducteur. Ces dé-
placements sont imposés par l’action de la force électromagnétique, dont l’interaction
avec la matière est le fondement de l’électricité.
Le courant électrique peut avoir différentes causes : un écoulement de particules
négatives ou un écoulement de particules positives, ou un écoulement de particules négatives et positives dans des directions opposées.
Pour réduire cette complexité, les électriciens emploient toujours la convention de
Franklin et, imaginent le courant électrique, connu sous le nom de courant conventionnel, comme constitué d’un écoulement de particules exclusivement positives.
Le courant conventionnel simplifie les concepts et les calculs, mais masque le
fait que dans quelques conducteurs (électrolytes, semi-conducteurs, et plasma)
les deux types de charges électriques se déplacent dans des directions opposées,
ou que dans les métaux, les charges négatives sont quasi exclusivement responsables de la circulation du courant. Ces derniers paramètres sont l’affaire des
scientifiques de recherche sur le sujet et des ingénieurs de conception en électrotechnique et électronique.
0.2.3 Tension, U of V (Volt,V)
La tension électrique représente le travail de la force électrique (qui règne au sein
du dipôle) sur une particule chargée, divisé par la valeur de la charge (dans le cas
d’un générateur de tension continue, une pile par exemple, la tension électrique
à vide de cette pile, appelée force électro motrice (fem), est le travail de la force
electro de propulsion sur les électrons). On parlera donc d’énergie échangée par
unité de charge, qui peut être comparée, si l’on ne tient pas compte des unités,
à l’énergie échangée pour une charge de 1 Coulomb. Son unité est donc celle
d’une énergie divisée par une charge électrique, c’est-à-dire, le Joule/Coulomb
qui équivaut à des Volts.
0.2.4 Conductivité, G(Siemens,S)
La conductivité électrique est l’aptitude d’un matériau à laisser les charges électriques se déplacer librement, autrement dit à permettre le passage du courant
électrique.
0.2.5 Résistance, R [Ohm,Ω]
C’est la propriété d’un matériau à s’opposer au passage d’un courant électrique.
La différence de potentiel ou tension U (en volts) aux bornes d’une résistance R
(en ohms) est proportionnelle à l’intensité du courant électrique I (en ampères)
qui la traverse.
0.2.6 Puissance, P [Watt, W]
En physique, la puissance est la quantité d’énergie par unité de temps fournie par
un système à un autre. La puissance correspond donc à un débit d’énergie : deux
systèmes de puissance différente pourront fournir le même travail (la même énergie), mais le système le plus puissant sera le plus rapide. On peut allors dire
P = U.I [W = V.A]
La résistance est responsable d’une dissipation d’énergie sous forme de chaleur.
Cette propriété porte le nom d’effet Joule. Cette production de chaleur est parfois
un effet souhaité (résistances de chauffage), parfois un effet néfaste (pertes Joule).
La puissance dissipée par effet Joule est
0.3 CIRCUITS AVEC DES RÉSISTANCES
0.3.1 Circuit en série.
En électricité, un circuit en série désigne un circuit électrique (ou une branche
d’un circuit électrique), où les composants (résistances, condensateurs, générateurs, etc.) appartiennent à la même branche. Pour que des éléments soient en
série il faut que les mêmes charges traversent les dits éléments.
Analyse
Dans un circuit, des dipôles sont en série si, et seulement si, ils sont traversés par
le même courant. L’intensité du courant traversant chacun d’eux est donc égale
soit I = I1 = I2 = ... = In
Figure 1: Une connexion de résistances en serie.
Pour une connexion de résistances en série la résistance équivalente (total) du
circuit est égale à:
Rtotal = R1 + R2 + .... + Rn
Cette équation peut être démontrée en se basant sur les propriétés du circuit:
Utotal = U1 + U2 + .... + Un
Itotal = I1 = I2 = ...In
En utilisant la loi d’Ohm et les deux énoncés ci-dessus:
Utotal = R1.I + R2.I + .... + Rn.I
0.3.2 Circuit en parallèle
En électricité, un circuit en parallèle est un circuit électrique dont les branches sont
connectées par des noeuds communs. Dans le cas d’un élément à deux bornes, les
éléments en parallèle partagent une paire de noeuds, trois pour un élément à trois
bornes et ainsi de suite.
Figure 2: Deux résistances en parallèle.
Figure 3: Courants dans un circuit en parallèle.
Analyse
Dans un circuit en parallèle, les branches sont soumises à la même tension mais
le courant n’est pas le même dans chaque branche (sauf cas particuliers). Pour un
noeud se divisant en n branches, on a la relation :
Inoeud = I1 + I2 + .... + In
où In est le courant qui traverse la branche n. Cette relation indique donc que
la somme des courants dans chaque branche est égale au courant de noeud. Ces
caractéristiques sur la distribution des courants et de la tension dans un circuit parallèle permettent de déduire les valeurs équivalentes d’éléments passifs linéaires
combinés en parallèle. Ces formules peuvent être utilisées lors de l’analyse d’un
circuit pour simplifier l’obtention de la solution.
Pour une connexion de résistances en parallèle, la résistance total est égale à:
La résistance totale équivalente est donc plus faible que chacune des résistances
individuelles composant le circuit. Dans le cas particulier où toutes les résistances
en parallèle sont de mêmes valeurs, la résistance équivalente sera égale à cette
valeur divisée par le nombre d’éléments en parallèle.
Cette équation peut être démontrée en se basant sur les propriétés du circuit:
Utotal = U1 = U2 =....= Un
Itotal = I1 + I2 + .... + In
En utilisant la loi d’Ohm et les deux énoncés ci-dessus on peut écrire:
0.3.3 Diviseur de tension
Le diviseur de tension est un montage électronique simple qui permet de diviser
une tension d’entrée. Un circuit constitué de deux résistances en série est par exemple un montage élémentaire qui peut réaliser cette opération. Il est couramment
utilisé pour créer une tension de référence ou comme un atténuateur de signal à
basse fréquence.
0.4 LOIS ET THÉORÈMES
0.4.1 Les lois de Kirchoff.
Les lois de Kirchhoff expriment la conservation de l’énergie et de la charge dans
un circuit électrique. Elles portent le nom du physicien allemand qui les a établies
en 1845 : Gustav Kirchhoff.
Dans un circuit complexe, il est possible de calculer les différences de potentiel aux bornes de chaque résistance et l’intensité du courant continu dans chaque
branche de circuit en appliquant les deux lois de Kirchhoff : la loi des noeuds et
la loi des mailles.
Loi des noeuds
La somme des intensités des courants qui entrent par un nIJud est égale à la somme
des intensités des courants qui en sortent. Les intensités des courants sont des
grandeurs algébriques (positives ou négatives). Sur la figure est représenté le sens
(choisi arbitrairement) des courants entrant ou sortant du nIJud A. D’après la loi
des noeuds, on a donc :i1 + i4 = i2 + i3. Cette loi découle directement de la
Figure 4: Schéma d’un montage électrique illustrant la loi des noeuds.
conservation de la charge électrique, en tenant compte du fait que ces charges
ne peuvent pas s’accumuler à un endroit quelconque du circuit. Les charges qui
arrivent à un nIJud compensent celles qui en repartent.
Loi des mailles
Figure 5: Schéma d’un montage électrique illustrant la loi des mailles.
Dans une maille quelconque d’un réseau, la somme algébrique des tensions le
long de la maille est constamment nulle. Cette loi découle de la définition de la
tension comme différence de potentiel entre deux points. La tension entre a et b
est U = V b − V a. Va et Vb étant les potentiels respectifs aux points a et b. En
additionnant toutes les tensions d’une maille et en se servant de cette définition,
on obtient un résultat nul.
Le théorème de Thévenin a été initialement découvert par le scientifique allemand
Hermann von Helmholtz en 1853, puis en 1883 par l’ingénieur télégraphe français
Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit
principalement des propriétés de linéarité[1] et du principe de superposition qui en
découle. Il s’utilise pour convertir une partie d’un réseau complexe en un dipôle
plus simple.
Un réseau électrique linéaire vu de deux points est équivalent à un généra
Figure 6: réseau équivalent.
teur de tension parfait dont la force électromotrice est égale à la différence
de potentiels à vide entre ces deux points, en série avec une résistance égale à
celle que l’on mesure entre les deux points lorsque les générateurs indépendants sont rendus passifs.
Détermination du modèle de Thévenin
Soit un circuit composé de plusieurs sources et de plusieurs résistances possédant
deux bornes A et B entre lesquelles est raccordée une charge :
1. La tension de Thévenin est la tension calculée ou mesurée, entre les bornes
A et B lorsque la charge est déconnectée (tension à vide). .
2. La résistance de Thévenin est la résistance calculée, ou mesurée, entre les
bornes A et B lorsque la charge est déconnectée et que les sources sont
éteintes : les sources de tension indépendantes sont remplacées par un courtcircuit et les sources de courant indépendantes par un circuit ouvert.
Example.
• Calcul de la tension aux bornes de AB.
Figure 7: Circuit originel.
(R1 Notez que R1 n’est pas prise en considération, car les calculs ci-dessus
sont faits en circuit ouvert entre A et B, par suite, il n’y a pas de courant qui
passe à travers R1 et donc aucune chute de tension n’y apparait)
Figure 8: Calcul de la tension aux bornes de AB.
• Calcul de la résistance équivalente aux bornes AB en court-circuitant V1.:
RAB = 2KΩ
Figure 9: Calcul de la résistance équivalente aux bornes AB en court-circuitant
V1.
• Circuit équivalent de Thévenin. Celui-ci nous permet de trouver aisément le
courant dans un dipôle quelconque relié entre les bornes A et B sans qu’on
ait à résoudre le circuit au complet.
Figure 10: Circuit équivalent de Thévenin.




















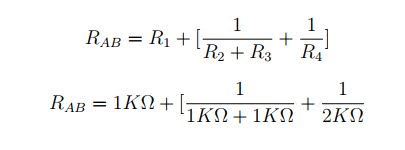



تعليقات
إرسال تعليق